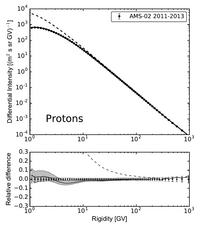
GALPROP obtained LIS using modulated spectra from HelMod
The local interstellar spectra (LIS) are input cosmic ray intensities for any modulation models. Fluxes are assumed isotropically distributed at heliosphere boundary, in a steady-state configuration. The LIS is usually computed using numerical model accounting for the propagation in galaxy. The heliosphere modulation is the added using, e.g.,the modulation module available here for on line use or download.
Recently, Boschini et al 2017, 2018a, 2018b, 2020a, 2020b deduced LIS's for protons, helium nuclei and antiprotons using the most recent experimental results combined with GALPROP model for propagation in galaxy and HelMod for the propagation in heliosphere.
Successive work extend the available sets of LIS's. Boschini et al 2018b, using the same procedure, deduced LIS's for Carbon- and Oxygen-nuclei, while Boschini et al 2018a deduced LIS for galactic electrons.
HelMod and GALPROP were combined to provide a single framework and run to reproduce a comprehensive set of observations of CR species collected in different time periods, from 1997 up to 2015.
The numerical table of computed LIS is available as supplementary material of Boschini et al 2017, Boschini et al. 2018a, and Boschini et al 2020b.
Antiproton LIS
Boschini et al 2017 provides analytical fits to the derived LIS. The fit to the antiproton LIS provides an accuracy of 2-3% for 3 GV \(<R<1000\) GV and 10% for 1.5 GV \(<R<3\) GV:
\begin{equation}
F(R)\times R^{2.7} = 1.34-4.99\times 10^{-4}R+\frac{44.3}{12.6+R}-\frac{168}{31.1+R^{2}} +\frac{13600}{22200+R^{2}}, \quad R>1.5\ {\rm GV},
\end{equation}
while the average accuracy of AMS-02 data is about 10%-20%.
Electron LIS
In Boschini et al 2018a., it was provided a parameterization \(F(T)\) of the electron GALPROP LIS from 2 MeV up to 90 GeV as a function of kinetic energy in GeV:
\begin{align}\label{EQ::ele}
&F(T) = \\
&\left\{
\begin{array}{ll}
\frac{1.181\!\!\times\!\! 10^{11} T^{-12.061}}{1+4.307\!\!\times\!\! 10^{8} T^{-9.269}+3.125\!\!\times\!\! 10^{8} T^{-10.697}} & T<6.88 GeV\,\\ \nonumber
995.598\, T^{-3.505}+4.423\, T^{-2.620}, & T\ge 6.88 GeV, \nonumber
\end{array}
\right.\nonumber
\end{align}
where the units are (m\(^2\) s sr GeV)\(^{-1}\). This fit reproduces the \galprop{} electron LIS with an accuracy better than 5\% for the whole quoted energy range.
The electron LIS that results from the model calculations is in a good agreement with data (See discussion in Boschini et al 2018a.). Meanwhile, it may harbor an additional electron component from an unknown source of the same nature as that of the excess positrons. If charge-sign symmetry is assumed, i.e. that the electron and positron components coming from an unknown source have identical spectra, then the spectral shape of such an additional electron component can be derived from AMS-02 positron measurements. The spectrum of an additional component, ``the signal,'' \(S(T)\) can be parametrized as a function of kinetic energy as:
\begin{equation}
S(T)= 4.5\times10^{-3}\ T^{-1.53} e^{-\frac{T}{400\ {\rm GeV}}}\ ({\rm m}^2\ {\rm s\ sr\ GeV})^{-1}
\end{equation}
This involves a re-tuning of the electron injection spectrum above the break at 95 GV (See discussion in Boschini et al 2018a.). This parameterization also takes into account the standard astrophysical background of secondary positrons evaluated to be \(\le\)6\% at 30 GeV.
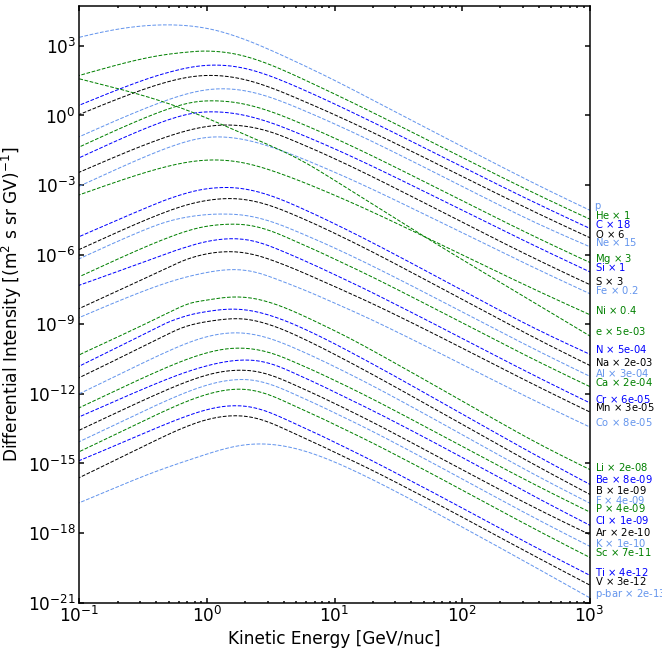
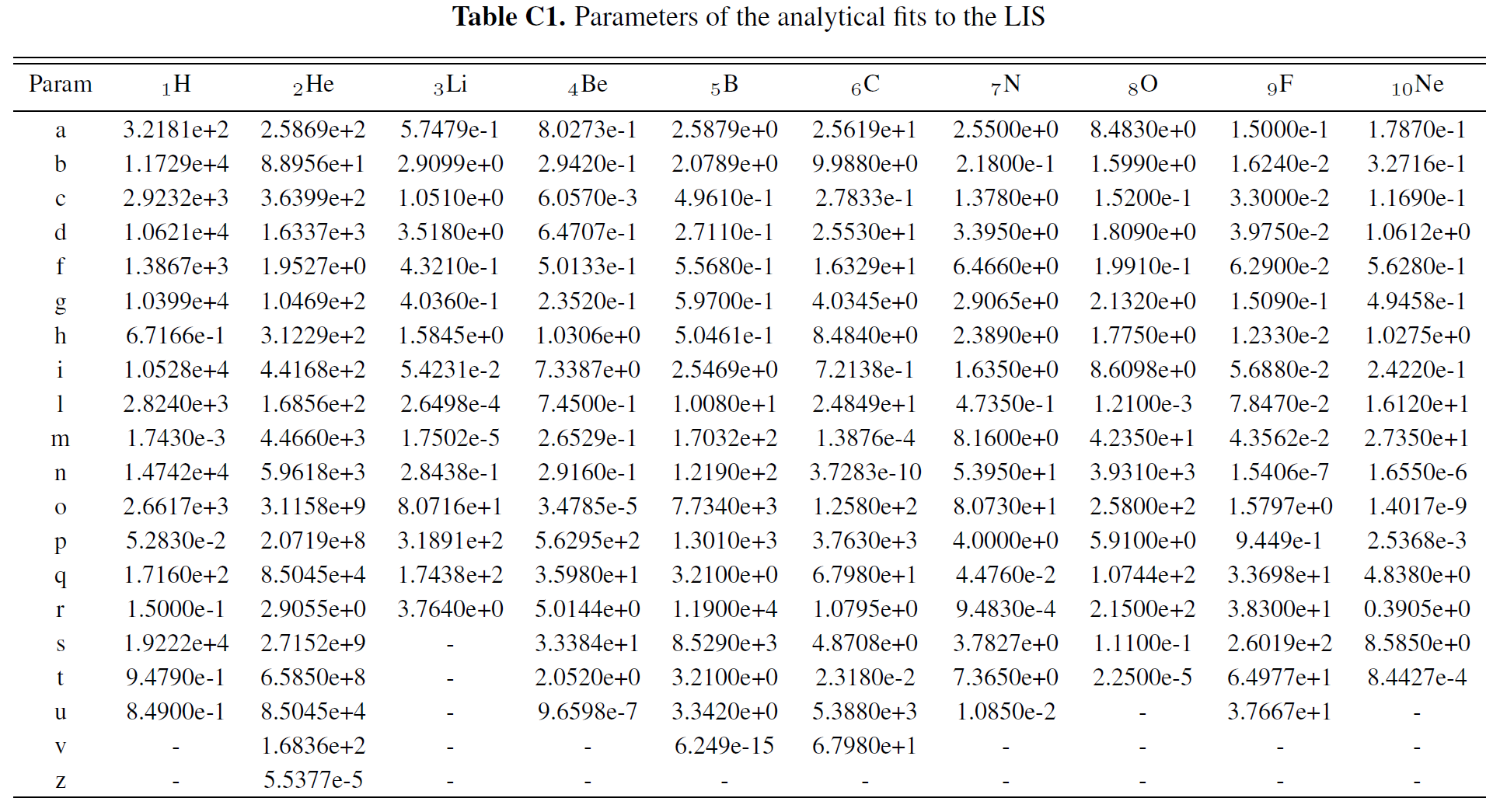
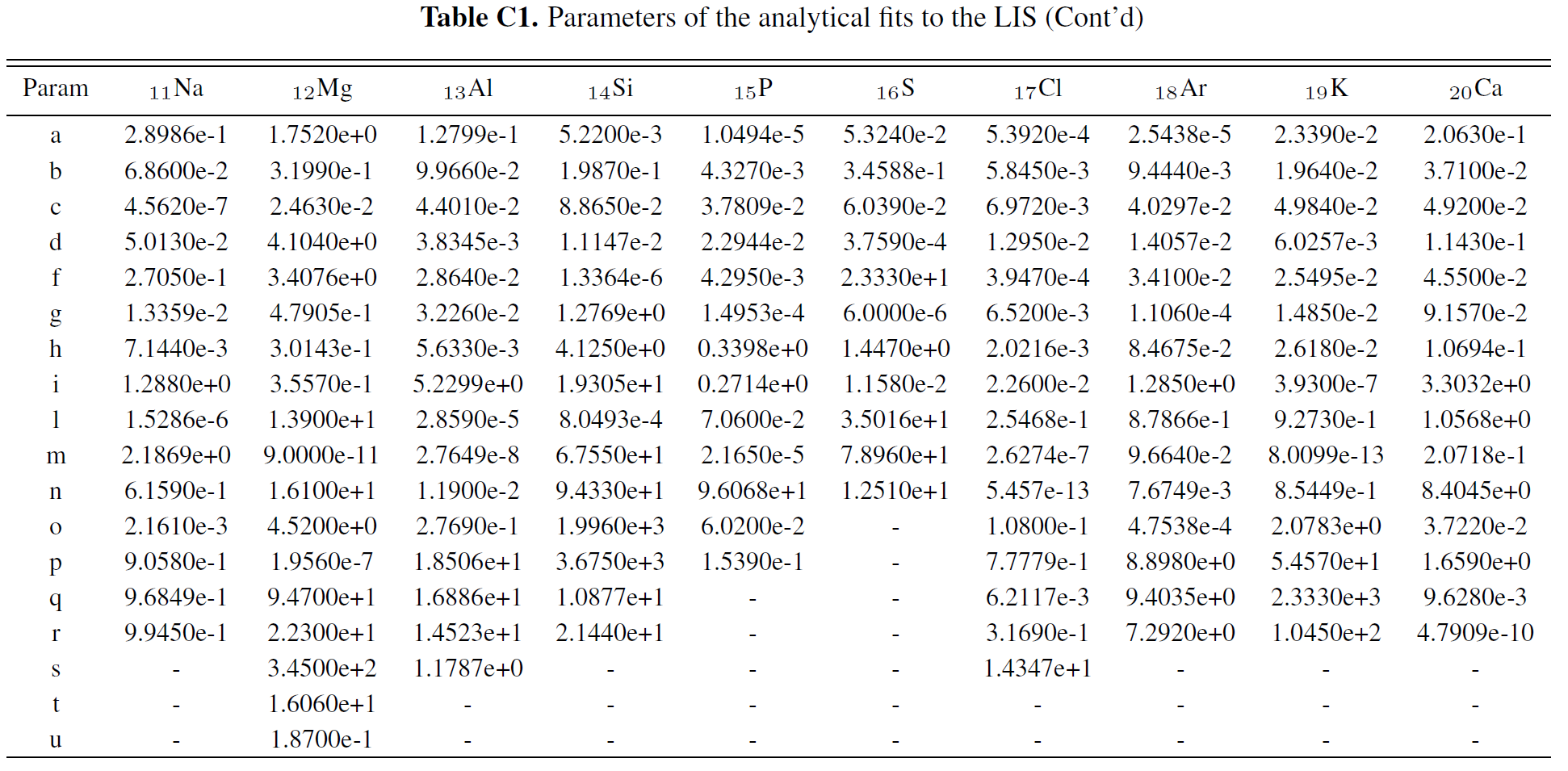
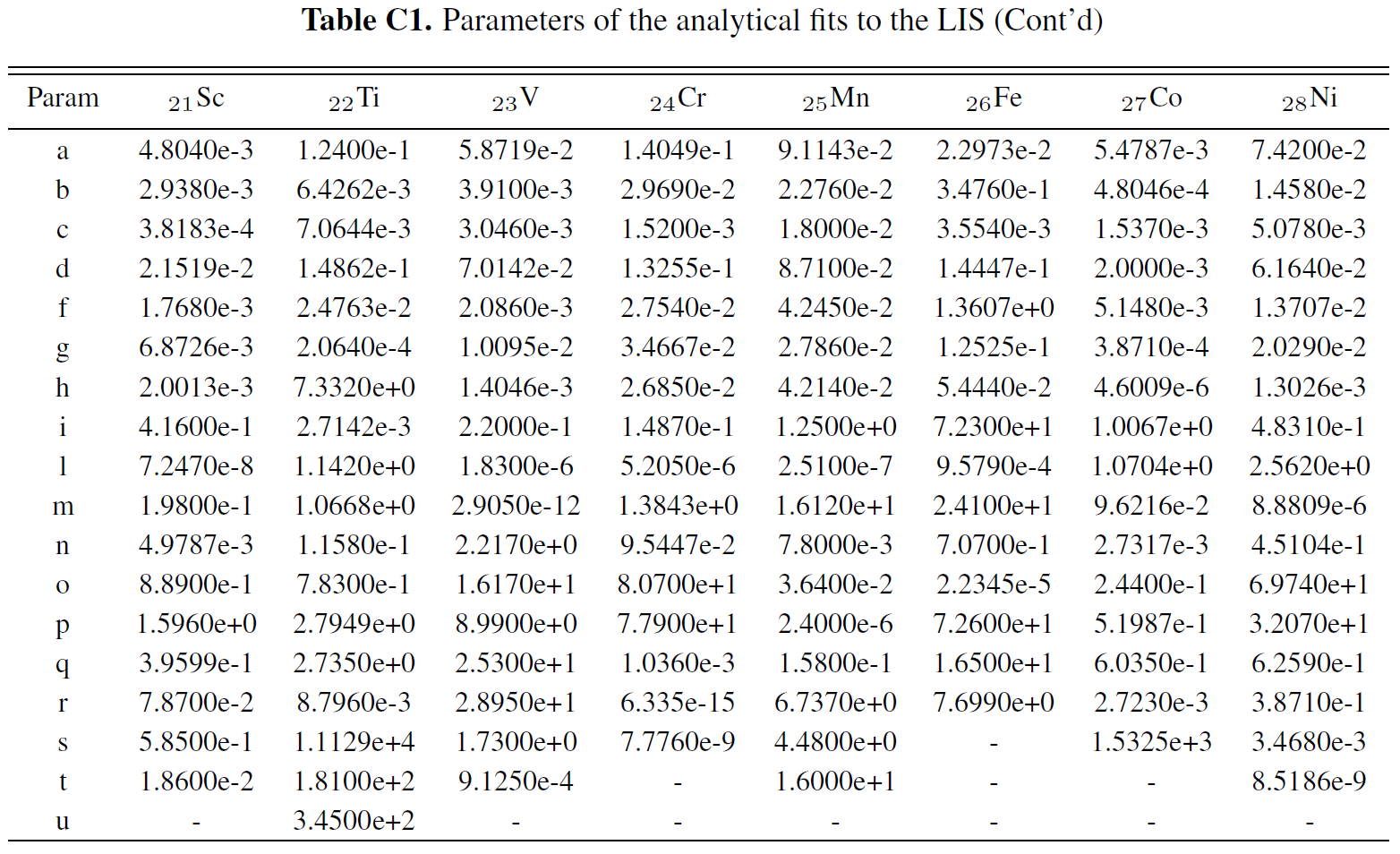
LIS for Proton and Nuclei up to Z<=28
Boschini et al 2020b provide analytical parameterizations of the LIS for each species, with parameters summarized inTable C1. The presented formulas parametrize numerical LISs obtained from the join effor of GALPROP and HelMod with an accuracy below 3% from 0.1 GV up to 105 GV and complete the numerical tables.
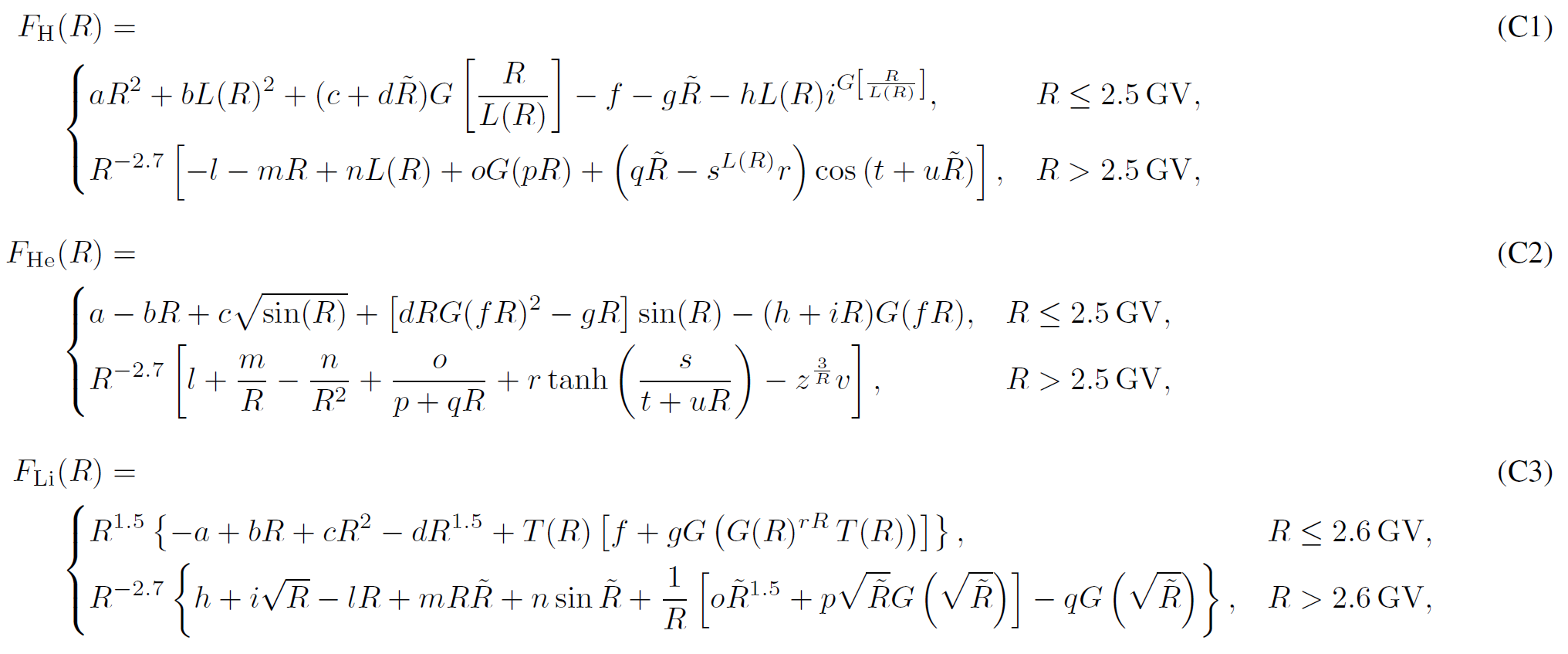
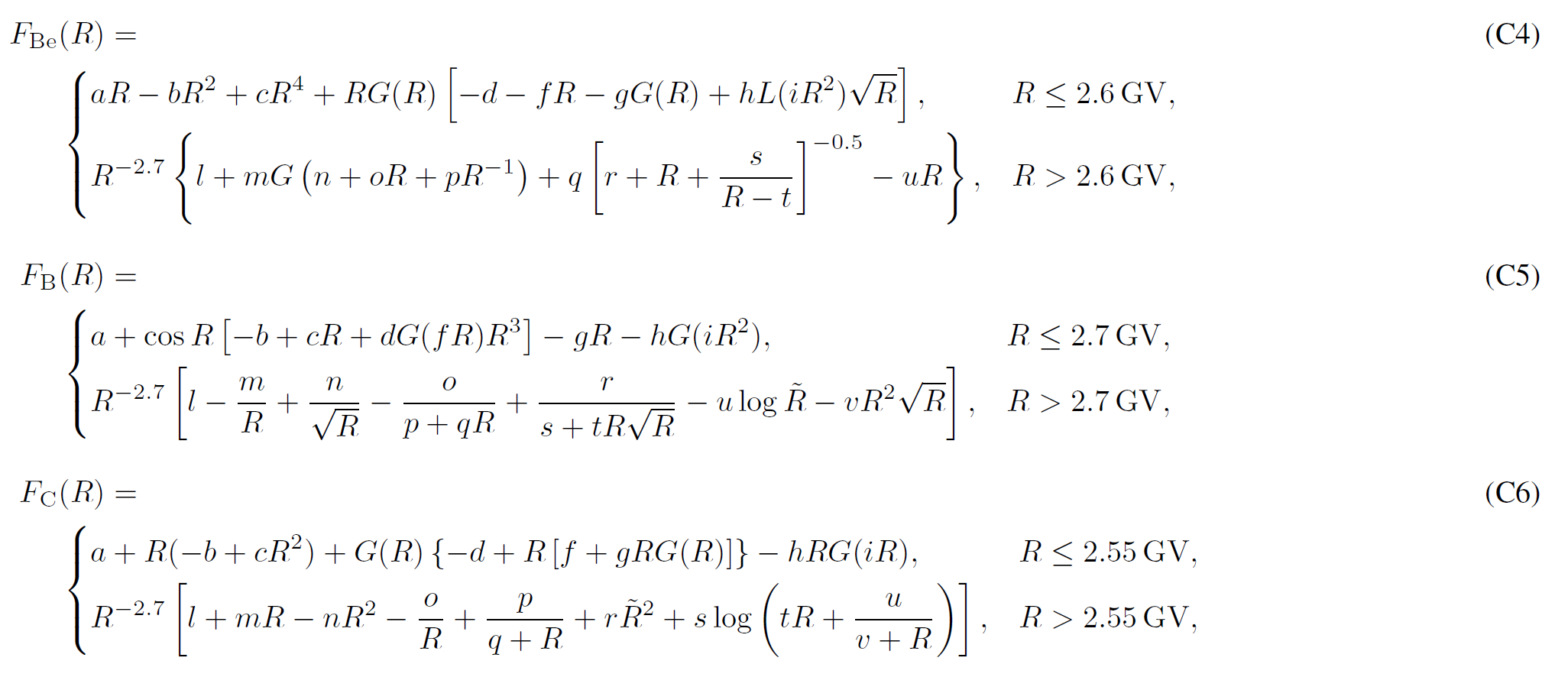
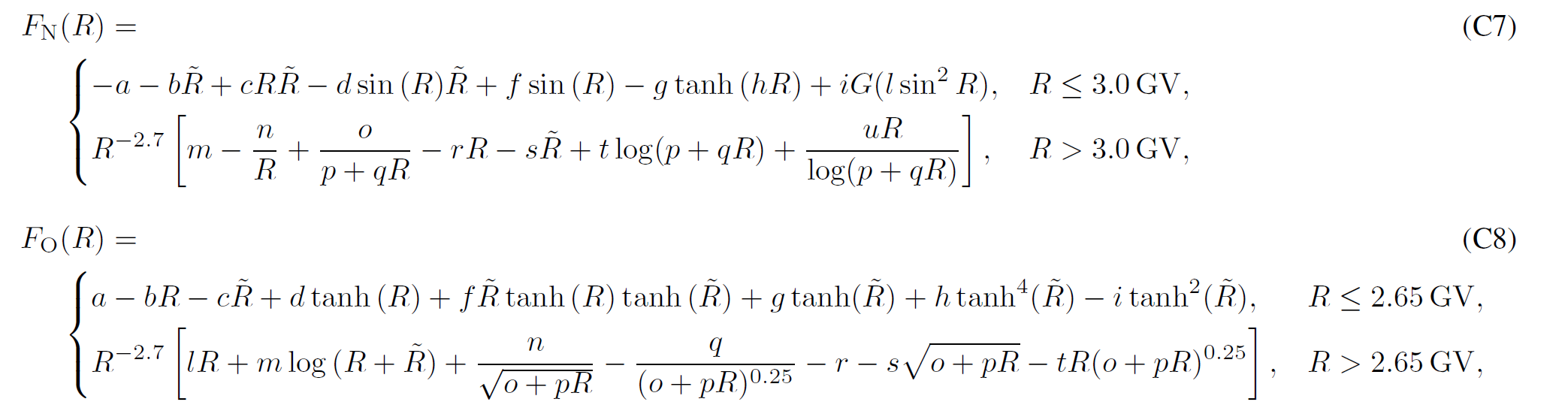
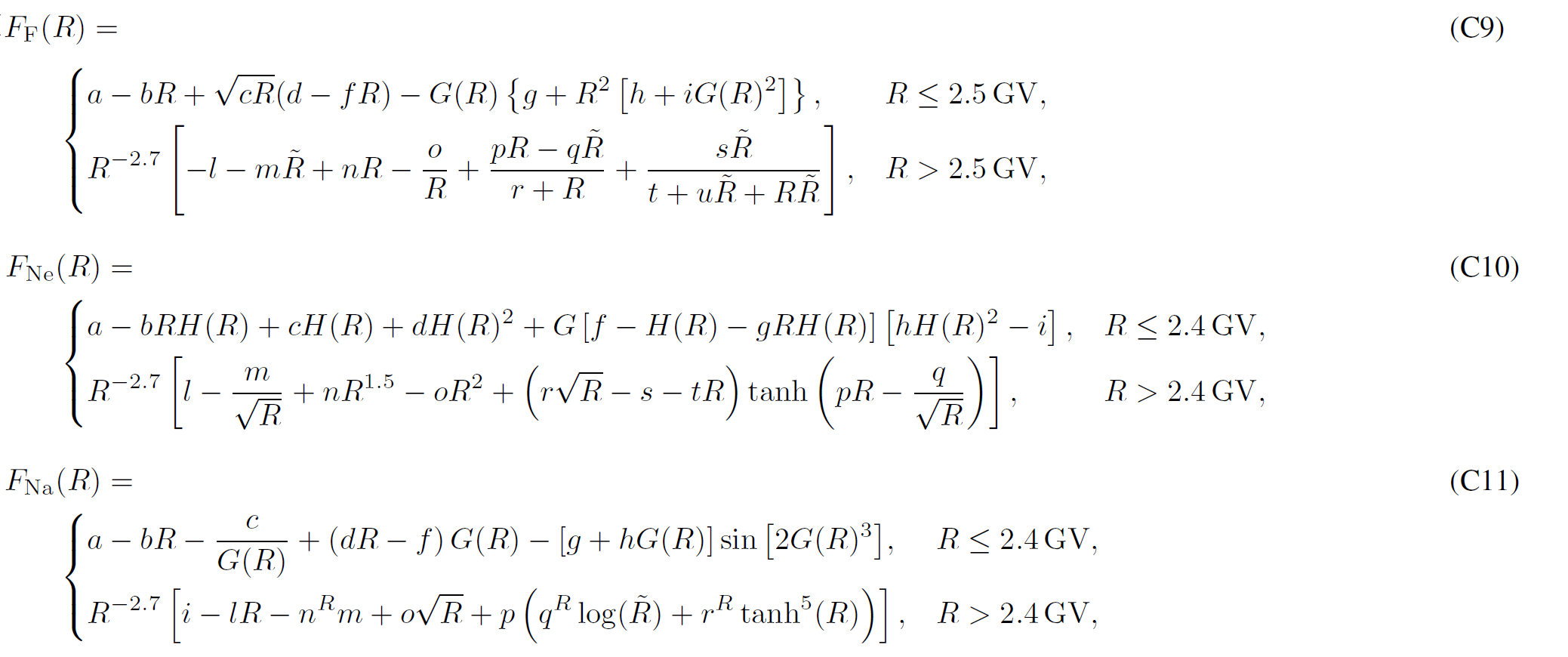
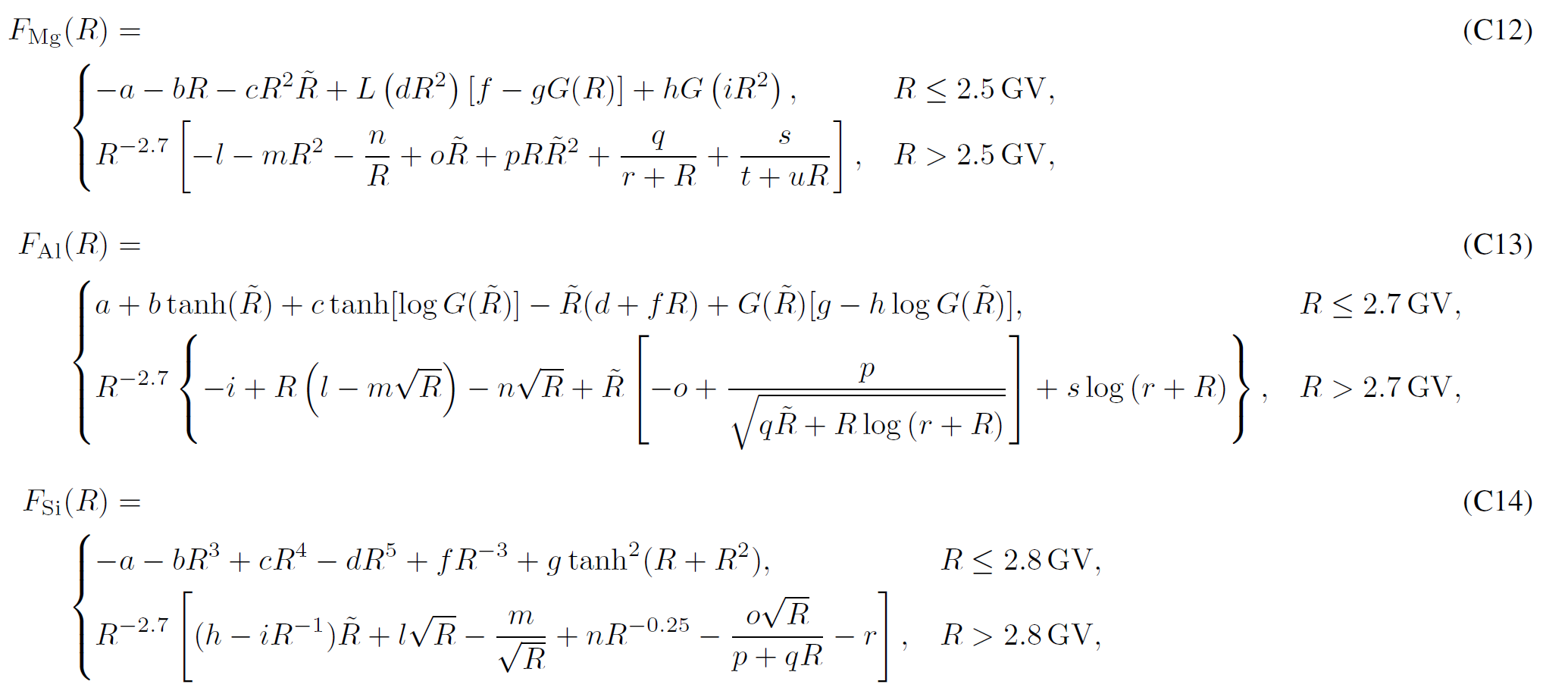
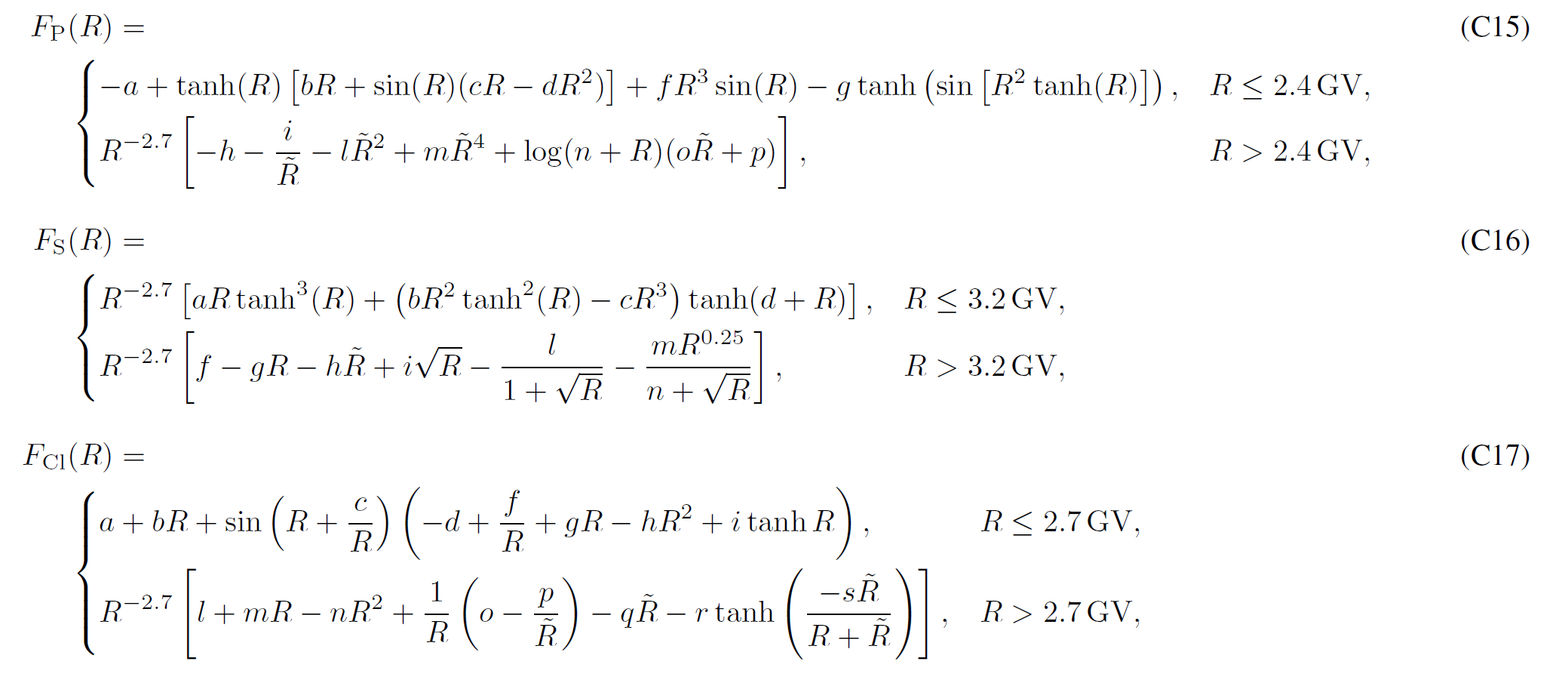
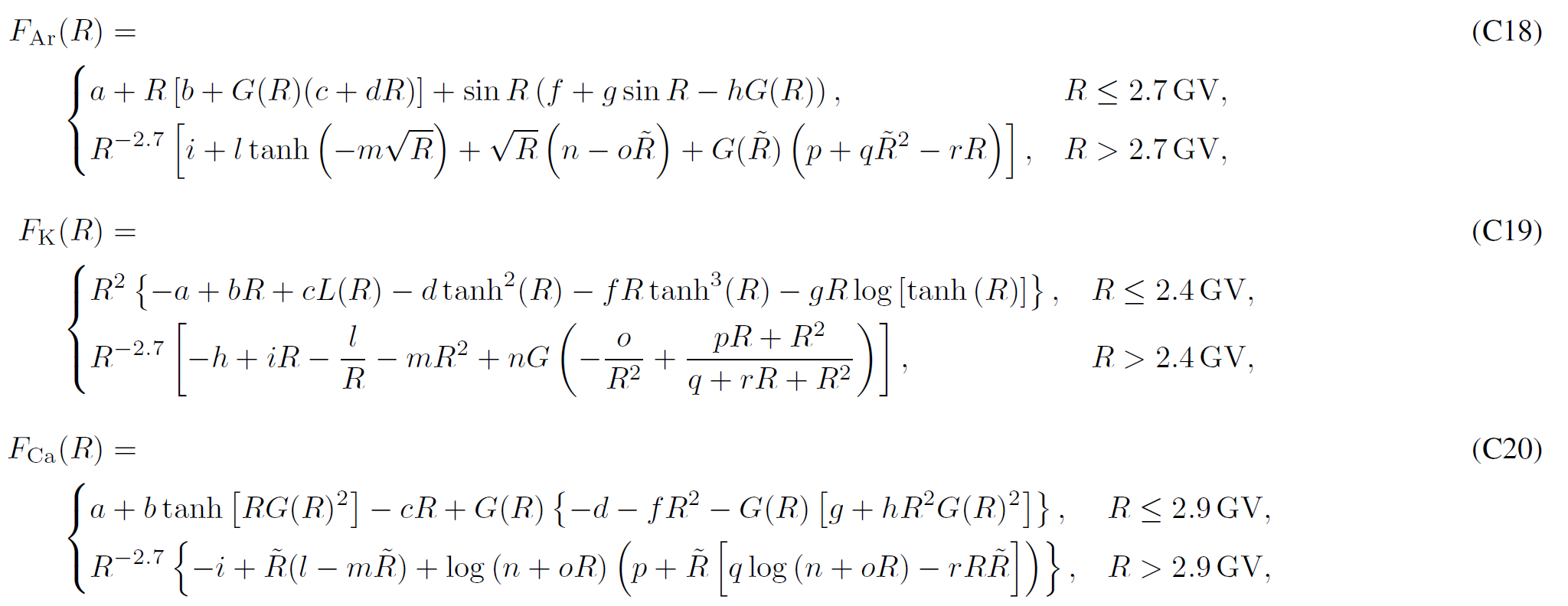
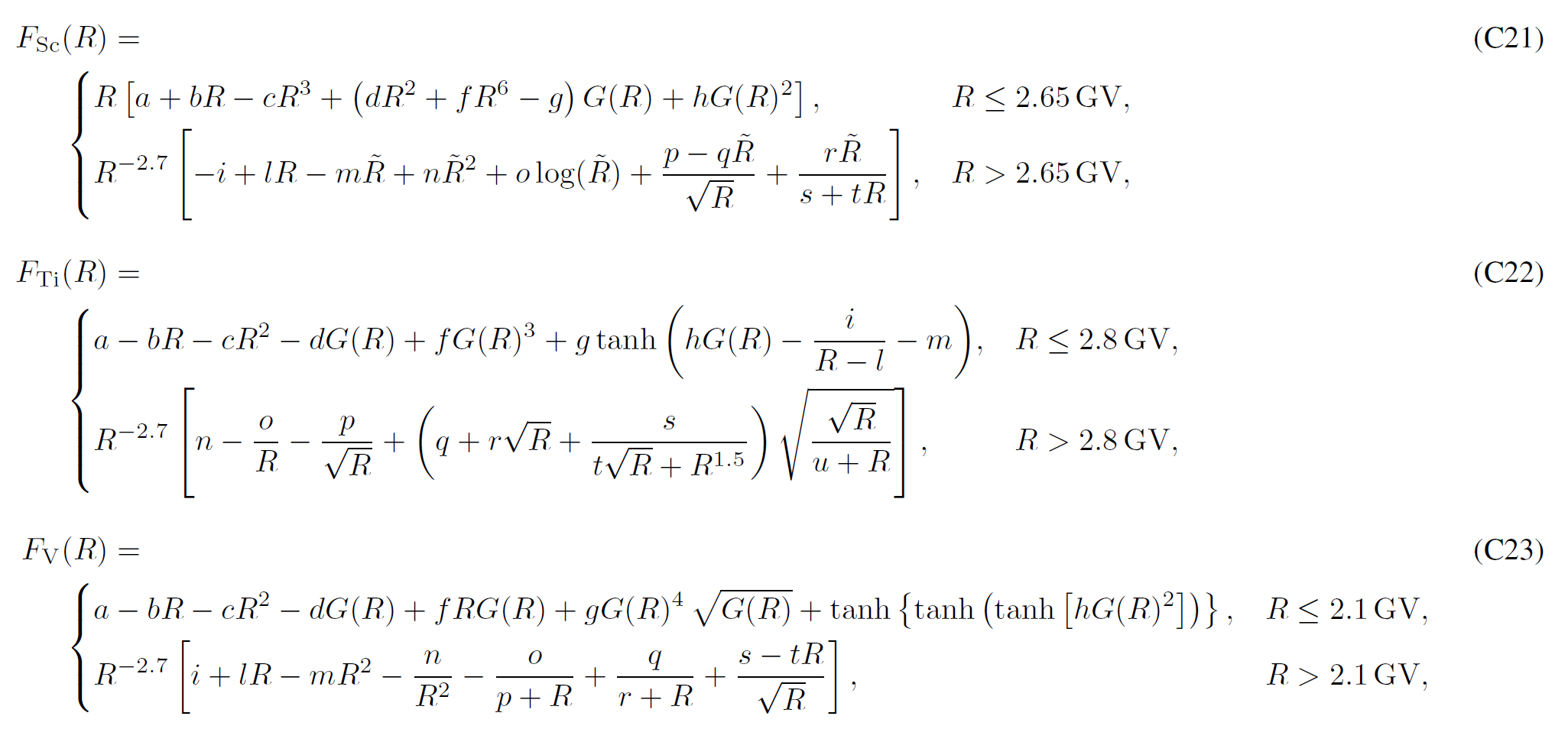
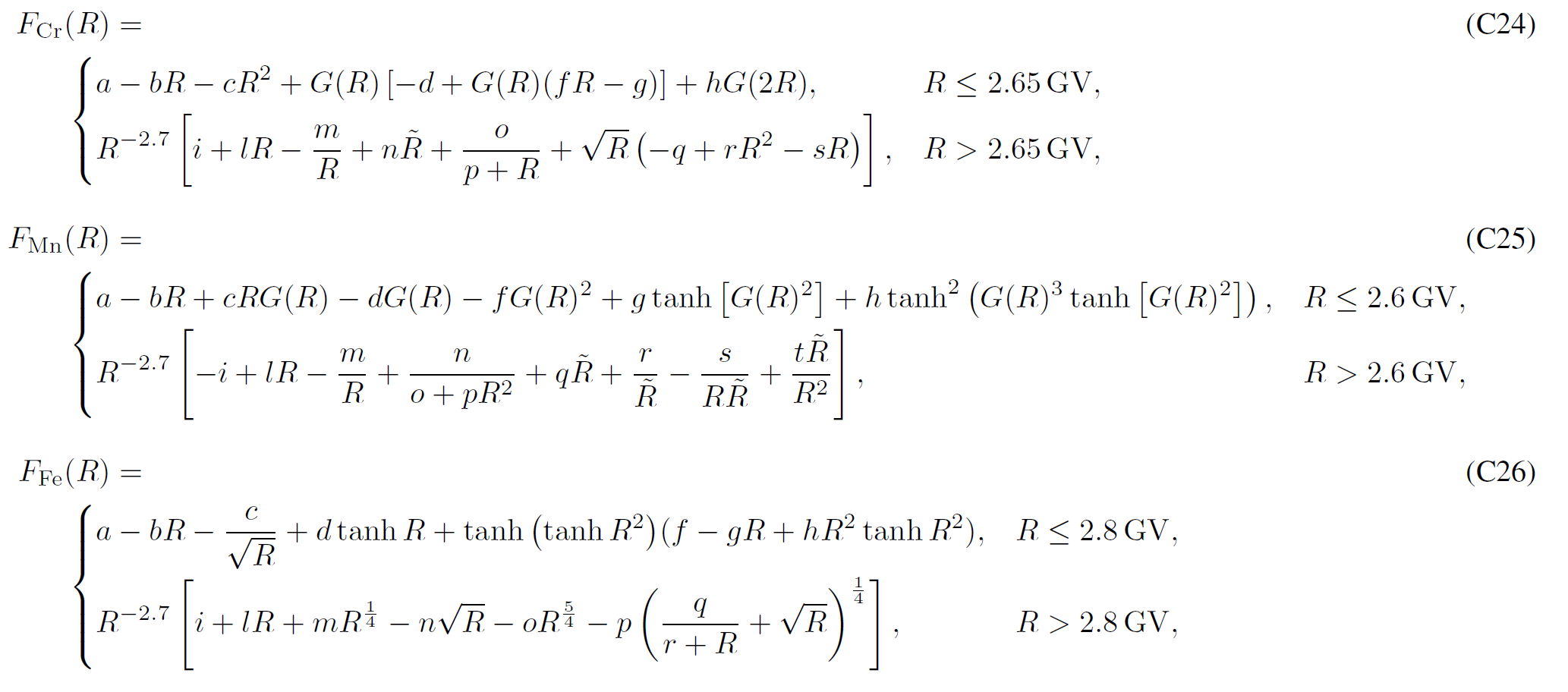
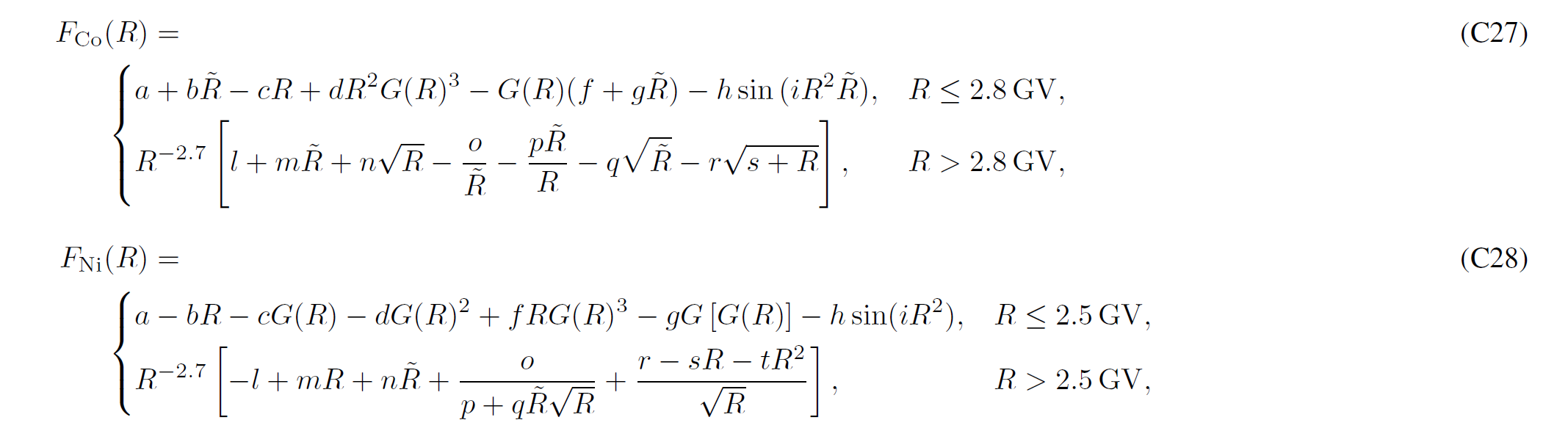

Bibliography
Currently published articles regarding local interstellar spectra (LIS):
- Solution of Heliospheric Propagation: Unveiling the Local Interstellar Spectra of Cosmic Ray Species Astrophys. J. 840:115, 2017
- HELMOD In The Works: From Direct Observations To The Local Interstellar Spectrum Of Cosmic-Ray Electrons Astrophys. J. 854:94, 2018
- Deciphering the Local Interstellar Spectra of Primary Cosmic-Ray Species with HelMod Astrophys. J. 858:61, 2018
- Deciphering the Local Interstellar Spectra of Secondary Nuclei with the Galprop/Helmod Framework and a Hint for Primary Lithium in Cosmic Rays Astrophys. J. 889:167, 2020
- Inference of the Local Interstellar Spectra of Cosmic-Ray Nuclei Z < 28 with the {GalProp}-{HelMod} Framework Astrophys. J. Supplement 250:27, 2020
- The Discovery of a Low-energy Excess in Cosmic-Ray Iron: Evidence of the Past Supernova Activity in the Local Bubble The Astrophysical Journal 913:5, 2021
- A Hint of a Low-energy Excess in Cosmic-Ray Fluorine The Astrophysical Journal 925:108, 2022
- Spectra of Cosmic Ray Sodium and Aluminum and Unexpected Aluminum Excess The Astrophysical Journal 933:147, 2022
- Spectra of He Isotopes and the 3He/4He Ratio The Astrophysical Journal 981:85, 2025