The following text is based on Boschini et al. (2024) and regards the HelMod-4/CUDA version for GPU architectures (see also Boschini et al. 2023, Della Torre et al. 2023).
As shown here, in HelMod the Parker transport equation is solved numerically by employing the Monte Carlo integration of an equivalent set of stochastic differential equations (SDE). The integration algorithm structure of SDE is very suitable for parallel computing, particularly GPU architectures. This property allows the possibility to design accelerated algorithms and then increase the performances of the computation.
In this field, the use of GPUs for this purpose represents a huge speedup in computing the GCR solar modulation, opening the feasibility of additional studies that need a large number of simulations and the systematical application to the assessment of space radiation effects considering those cases like deep-space missions for which GCRs are largely contributing to hazard. In fact, assessing the GCR contribution to the space radiation environment is a complex operation due to the time variability of GCR flux. Physically motivated models like HelMod-4 are key tools used to describe the transport of particles through the interplanetary medium. These methods have been used up to now only by specialists due to the long computational effort needed. Now, thanks to GPU algorithms like the one presented in this paper, these models will surely become achievable by general-purpose users.
In this section, we present the results of the GPU-accelerated algorithm applied to the HelMod-4 model. In Section 1, it is shown that HelMod-4 and HelMod-4/CUDA can be equivalently used to provide solar-modulated spectra with a similar degree of accuracy in reproducing observed data. In addition, the observed performances of the GPU algorithm represent a huge improvement with respect to the initial HelMod-4 code, quantified as an average improving factor of ~40 in run speed-up for the case of 5000 quasi-particles, as shown in Section 2. A complete description of the GPU implementation can be found in Boschini et al. (2024). In Section 3 the GPU farm at the University of Milano Bicocca is described.
1. Algorithm validation
To validate HelMod-4/CUDA we compared the numerical result with those obtained by HelMod-4 on CPU architecture.
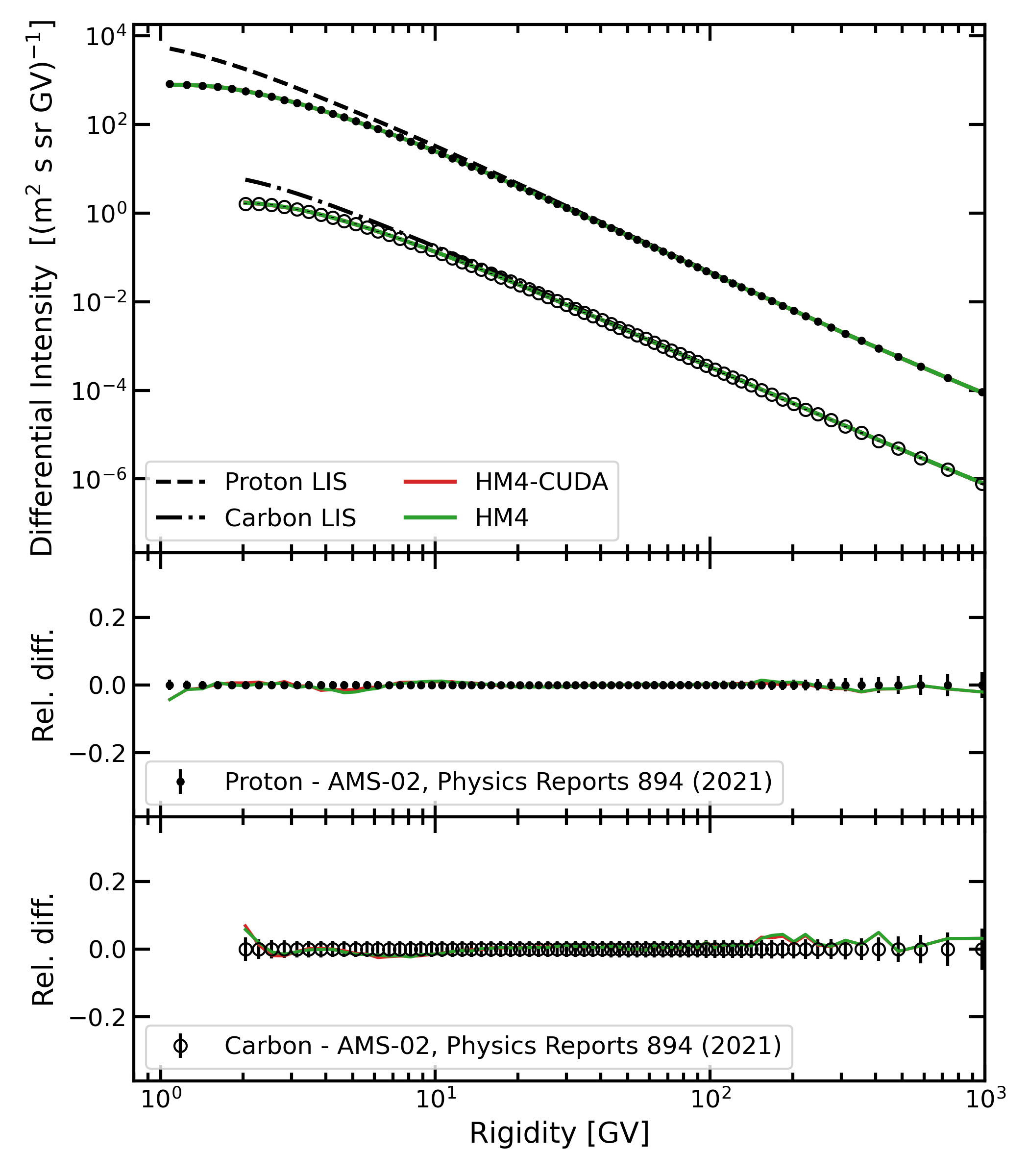
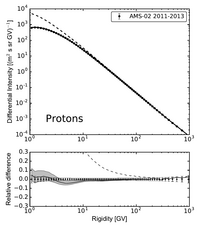
Fig. 1. Top panel: Modulated differential intensity of GCR proton and carbon spectra as obtained from HelMod-4 (green) and HelMod-4/CUDA (red) for the integrated period 2011–2018. Dashed and dot-dashed lines represent, respectively, the proton and the carbon LIS as defined in Boschini et al. (2020b). Black points and empty circles represent, respectively, proton and carbon spectra as measured by AMS-02 and reported in Aguilar et al. (2021). The color code is the same in the other panels of this figure. Middle (Bottom) Panel: Relative difference of HelMod-4 (HM4) and HelMod-4/CUDA (HM4-CUDA) modulated spectra with AMS-02 protons (carbon) observations, whose relative uncertainties are reported in black, for the same time interval. In all panels, red and green curves almost overlapped since the differences between HM4 and HM4-CUDA are below a few percent and experimental uncertainties. [Figure from Boschini et al. (2024)]
In Fig. 1 we show modulated spectra of proton and carbon GCR measured by AMS-02 (Aguilar et al., 2021) along with the differential intensities computed by HelMod-4 (green) and HelMod-4/CUDA (red) for the same period. The second and third panels of Fig. 1 report the relative difference of simulations from experimental data. From this figure, it is hard to distinguish results coming from the two algorithms. Differences are consistent with the uncertainties due to simulated statistics in the Monte Carlo solvers. The same comparison was performed, providing similar results, with all the experimental datasets used to validate the HelMod-4 model within the HelMod-GALPROP framework.
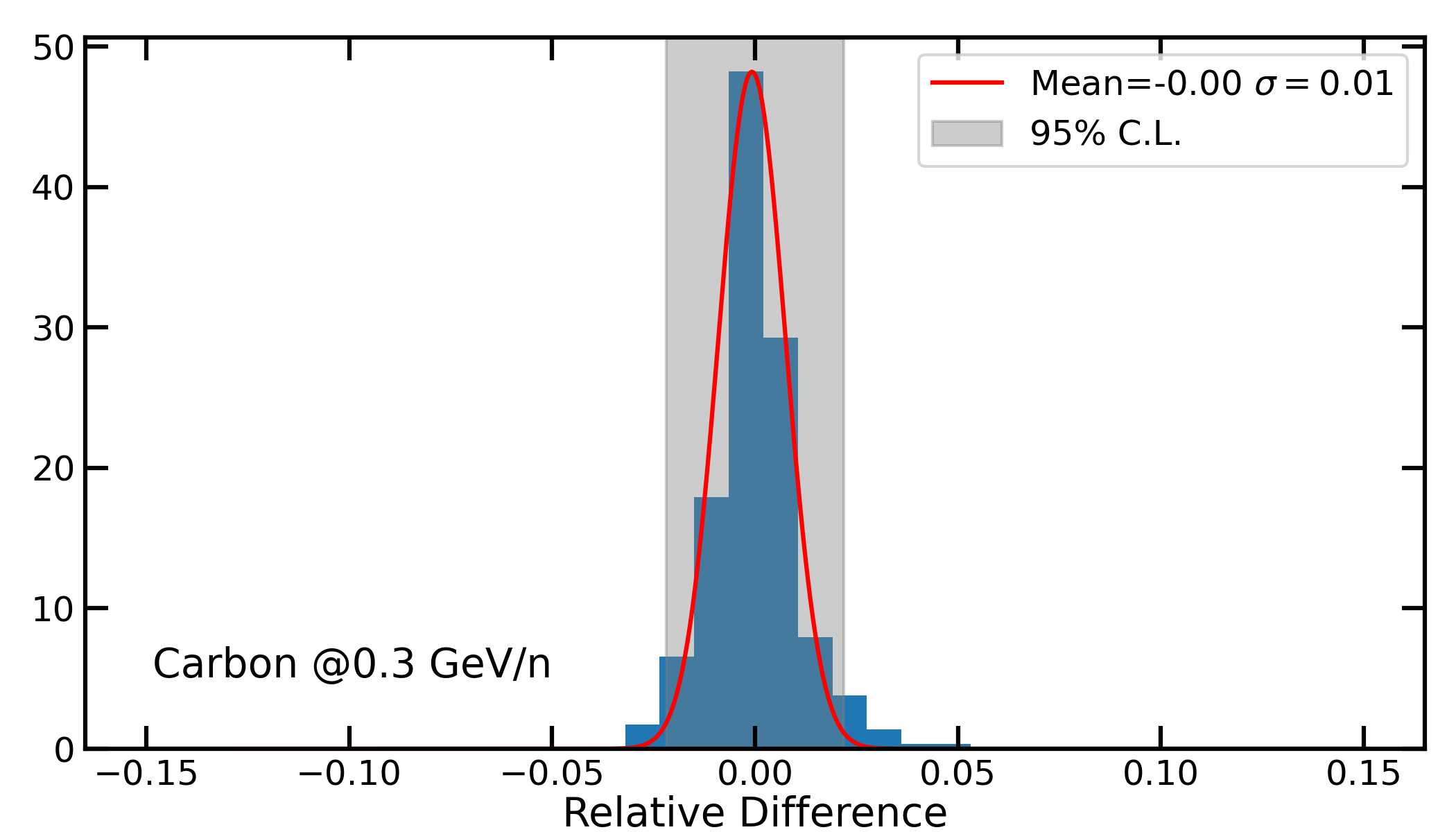
Fig. 4. Relative difference of HelMod-4/CUDA results with respect to the HelMod-4 ones. The left panel summarizes the mean relative differences computed for each bin in the time interval from 2020 to 2046. The values are computed for proton-, carbon-, silicon- and iron-modulated spectra. The horizontal dashed black lines mark the ∼ 2% uncertainty level. The right panel reports an example of how each point in the left panel is computed: for each energy bin we evaluated the distribution of the relative differences of the algorithms in the time interval 2020–2046 for each Carrington rotation. Then, the mean and standard deviation are computed. In this plot, we superimposed a Gaussian fit and the grey band represents the 2-σ uncertainty. [Figure from Boschini et al. (2024)]
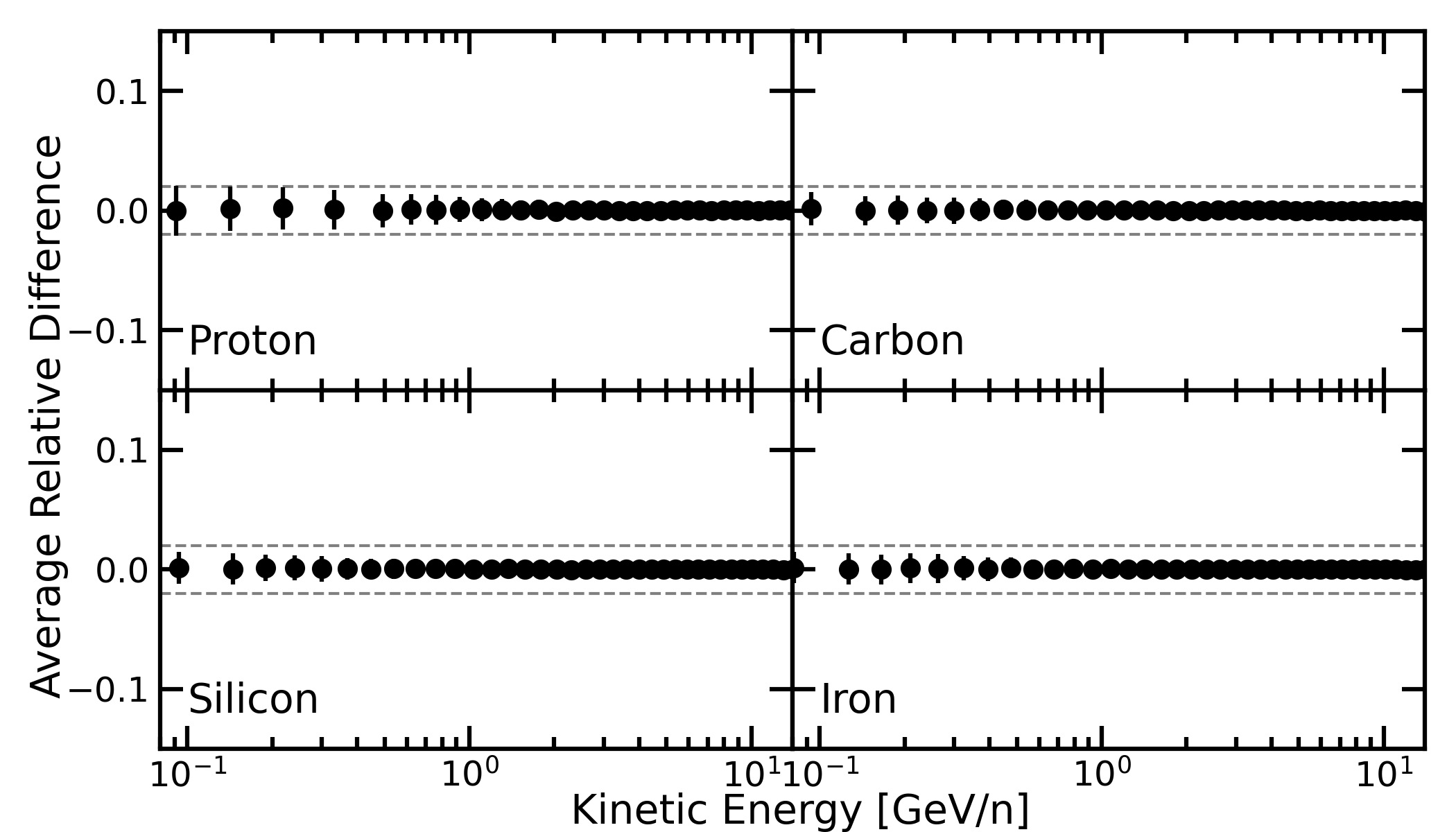
For a more general comparison, we considered the period 2020--2046 and the energy range from 0.1 to 20 GeV/n. This period covers a complete solar cycle in both polarities and considers the two typical usages of HelMod-4: reproducing past measurements and forecasting GCR intensities for future space missions (for a discussion on how the forecast is implemented in HelMod-4 see here). Each simulation was compared bin-by-bin to compute the relative difference of HelMod-4/CUDA results with respect to the HelMod-4 ones (see Fig. 2 - left). For each bin, the mean relative difference and the standard deviation were computed. As reported in Fig. 2 - right, representative of a typical result, the relative differences are distributed normally around zero. This means that the new algorithm does not introduce a significant systematic difference from the CPU one.
The results of this comparison, for all energy bins, are summarized in Fig. 2 - left for four of the most abundant GCR species (proton, carbon, silicon, and iron). The fact that the relative difference between the two algorithms is well confined within the 2% bands (horizontal dashed black line) is proof of the equivalence of the Monte Carlo solvers. All the other ions behave similarly. In other words, HelMod-4 and HelMod-4/CUDA can be equivalently used to provide solar-modulated spectra with a similar degree of accuracy in reproducing observed data.
2. Code Performances
The main motivation for developing a GPU-accelerated algorithm is the boost in performance. In this section, we show the performance of HelMod-4/CUDA algorithm with respect to HelMod-4 (i.e. the CPU code version) using the same parameters.
HelMod-4 was executed on a server with two CPU Intel(R) Xeon(R) 2.10GHz. Since the algorithm used by HelMod-4 does not use any software parallelization technique (i.e. each program uses one CPU-core), we recursively execute at the same time 30 \helmodf{} instances in order to not saturate the CPU resources.
HelMod-4/CUDA was executed on the same server with two GPU NVIDIA A30 Although HelMod-4/CUDA was designed to use all GPUs available, for these tests we forced the code to use only one GPU, allowing it to execute at the same time 2 HelMod-4/CUDA instances. Moreover, the code was compiled with the compilation flag --use_fast_math which would result in lower numerical accuracy but with a huge improvement in reducing the run time.
To evaluate the code performances under different working conditions, we computed the execution time of several energy bins and with a different number of quasi-particle objects from N=102 to 105. This measurement is obtained by averaging over ~200 HelMod instances. In this study, we considered 3 different Carrington rotations (i.e. CR numbers CR-1937, CR-2091, and CR-2132) corresponding to two consecutive solar minima (with opposite solar polarity) and a solar maximum period. The results among the three different periods are qualitatively similar, producing the same relative dependence from N but with different absolute normalization due to the different modulation parameters.
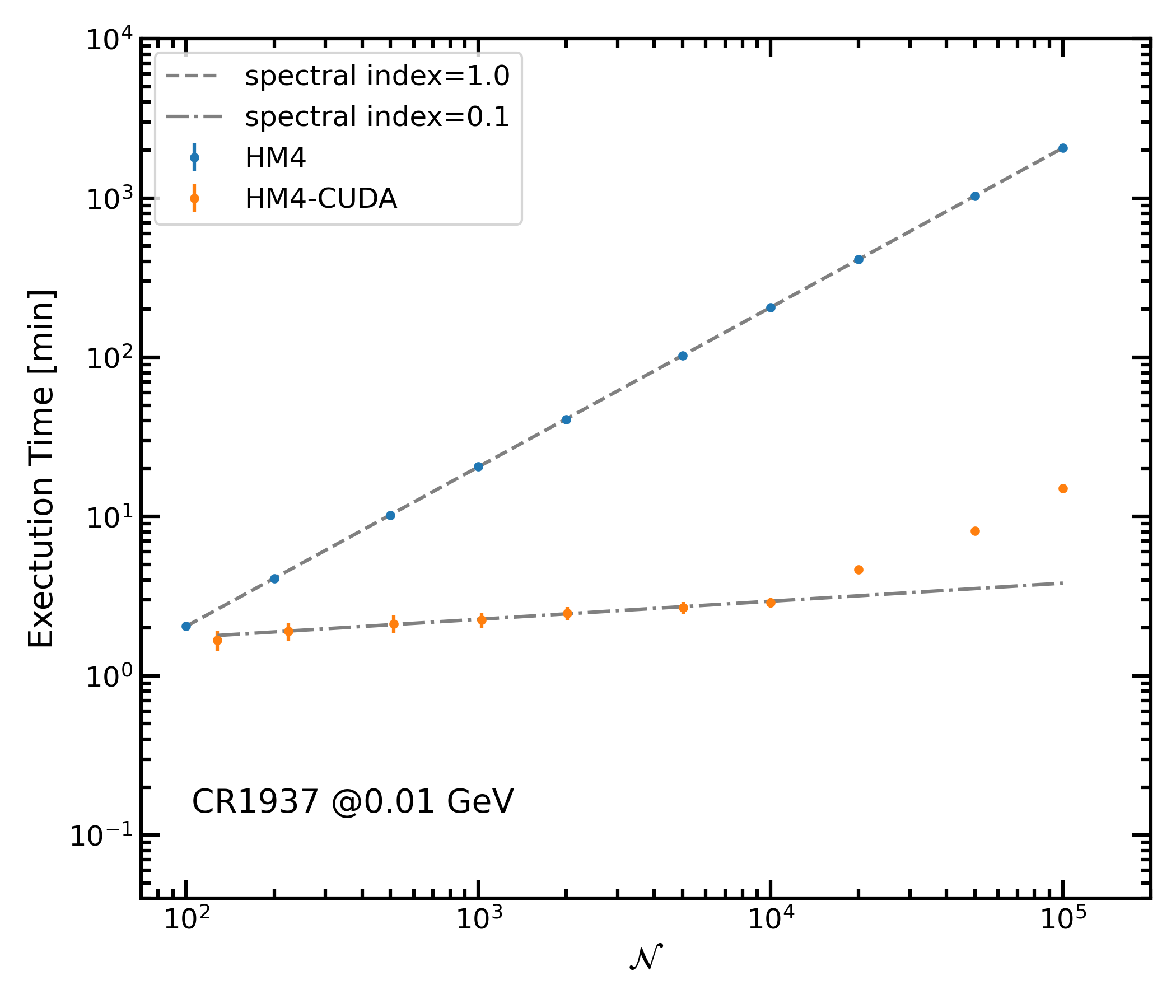
Fig. 3. HelMod-4 (blue points) and HelMod-4/CUDA (orange points) execution time in minutes with respect to the number of simulated events N for the case of 0.01 GeV GCR protons at Earth orbit on CR-1937. The grey lines represent the linear fit of the point in the N-range 102 ∼ 104. HelMod-4/CUDA execution times are evaluated by using 1 GPU board. [Figure from Boschini et al. (2024)]
In Fig. 3 the execution time in minutes of the two algorithms is shown as a function of N. Due to the linearity of the algorithm, the execution time of HelMod-4 scales as a power law of N with spectral index 1, i.e. a linear function. On the other hand, the execution time of HelMod-4/CUDA shows two different regimes: up to N~104 it scales as a power law with spectral index ~0.1, then the spectral index becomes steeper. This is because at N~104 the program saturated the GPU resources and additional operations are required. At N~105 we also register sporadic illegal memory errors. The observed performances represent a huge improvement with respect to the initial HelMod-4 code.
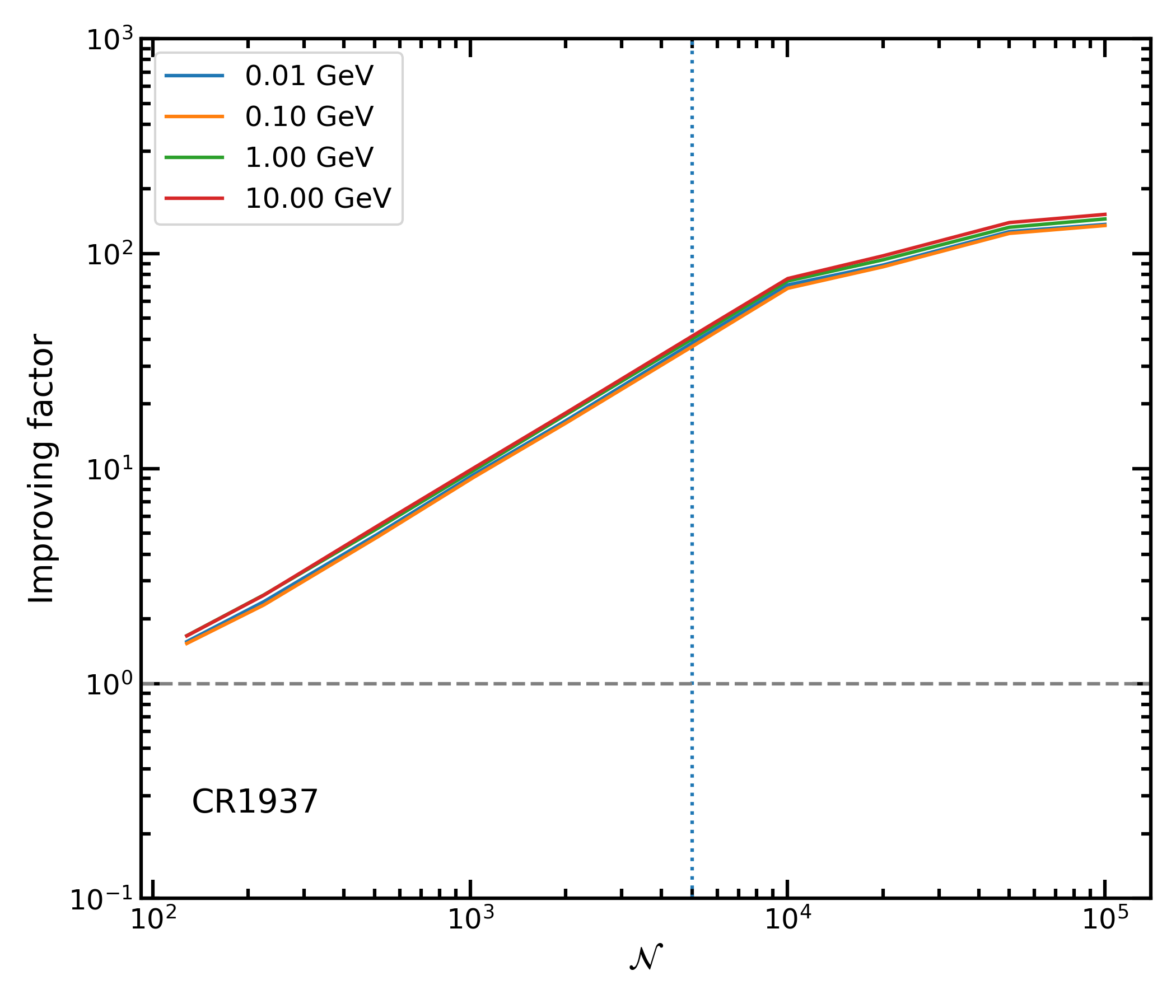
Fig. 4. Improving factor in processing speed by using GPU algorithm with respect to the CPU one. Simulations are performed for GCR protons at Earth orbit on CR-1937 and for four different initial energies. The factor is computed by the ratio of points in Fig. 3 interpolated to match the same N-value. [Figure from Boschini et al. (2024)]
In Fig. 4 we reported the improving speed-up factor evaluated as the ratio between HelMod-4 and HelMod-4/CUDA execution time for proton GCR during the CR-1937 for several kinetic energy. The results for CR-2091 and CR-2132 are similar and confirm an average improving factor of ~40 in run speed-up for the case of N~5000. One has to note that a similar improvement factor could be obtained also by a proper CPU paralleling algorithm, using all the available CPU cores. Anyway, the availability of high-performance GPUs at affordable cost makes the GPU solution very competitive. In addition, the possibility to install several GPUs on a relatively small cluster, if compared with a configuration hosting the same number of CPU cores, makes this solution also much more reliable in terms of requested room, power, and services.
3. GPU Farm
A dedicated ASIF datacenter with 10 NVIDIA GPUs was deployed at the University of Milano-Bicocca, additional GPU cards will be available soon.

Bibliography
Aguilar, M., Ali Cavasonza, L., Ambrosi, G. et al. (2021).Aguilar, M., Ali Cavasonza, L., Ambrosi, G. et al. (2021). The Alpha Magnetic Spectrometer (AMS) on the International Space Station: Part ii – results from the first seven years. Physics Reports, 894, 1 – 116. doi:10.1016/j.823 physrep.2020.09.003.824
Boschini, M., Della Torre, S., Gervasi, M. et al. (2023). Predicting galactic cosmic ray intensities in the heliosphere employing the HelMod model. In Proceedings of 38th International Cosmic Ray Conference —PoS(ICRC2023) (p. 1289). volume 444. doi:10.22323/1.444.1289
Boschini et al (2024), Fast and accurate evaluation of deep-space galactic cosmic ray fluxes with HelMod-4/CUDA, M. J. Boschini, G. Cavallotto, S. Della Torre, M. Gervasi, G. La Vacca, P. G. Rancoita, M. Tacconi, Advances in Space Research, April 2024, In Press
Della Torre, S., Cavallotto, G., Besozzi, D. et al. (2023). Advantages ofGPU-accelerated approach for solving the Parker equation in the heliosphere. In Proceedings of 38th International Cosmic Ray Conference —PoS(ICRC2023) (p. 1290). volume 444. doi:10.22323/1.444.1290.