The following text is based on / Extracted from Boschini et al 2019 and regards HelMod version 4 and beyond.
The boundary of the heliosphere, called heliopause (HP), is a contact discontinuity separating the solar cavity -- in which the SW plasma is flowing -- from the interstellar space. It also represents the extreme limit beyond which solar modulation does not affect CR flux. Thus, outside HP the truly pristine LIS of GCR spectra could be observed. After being accelerated in the solar corona (Parker, 1958) SW adiabatically expands in radial direction with supersonic speed. In its journey towards the external regions of the heliosphere SW flow changes its supersonic regime, through the formation of a physical boundary called Termination Shock (TS) which, in practice, separates the inner part of the heliosphere1 from the outer region2, also known as heliosheath (HS).
The heliosphere boundaries (i.e., TS and HP) were extensively discussed in the literature (e.g., Parker, 1961,1963; Axford, 1972; Holzer, 1989; Zank, 1999,2015 and references therein). Recently, fundamental advancements in the knowledge of the outer heliosphere were achieved by means of both Voyager probes, which provided on-site observations of TS and HP positions, SW plasma and magnetic field properties (e.g., see Richardson et al, 2008; Richardson, 2013,Nasa-Voyager,Burlaga and Ness, 2016,Nasa-OMNIWeb). In Parker's model of the heliosphere (Parker, 1961, 1963), such pieces of information can be exploited for allowing us to estimate the time dependence of both TS and HP positions -- i.e., those currently used in HelMod --, as discussed in Heliospheric boundaries section. For instance, the predicted TS values are in good agreement with those observed: for Voyager 1 (Voyager 2) the detected TS position is 93.8 AU (83.6 AU) and the predicted is 91.8 AU (86.3 AU), i.e. within 3 AU; and, using the HP position observed by Voyager 1, the predicted value is 120.7 AU at the time of the Voyager 2 HP crossing which occurred at 119 AU. Furthermore, the interstellar magnetic field strength measured by Voyager 1 is \((0.48\pm0.04)\)nT (Burlaga e Ness, 2016). In the context of the Parker model, at the TS positions observed by Voyager 1 and Voyager 2, such a magnitude requires that the value of the dimensionless stagnation pressure (Parker, 1963) approaches its maximum value, i.e., the one allowed for a spherical diamagnetic solar cavity (see discussion in Heliospheric boundaries section). It should be remarked that, from the measurements of energetic neutral atoms by IBEX (McComas et al, 2009) and Cassini (Krimigis, 2009), Dialynas et al. (2017) strongly suggested a diamagnetic bubble-like heliosphere3 with negligibly small tail-like features (see also Drake, 2015,Opher et al 2015, 2017).
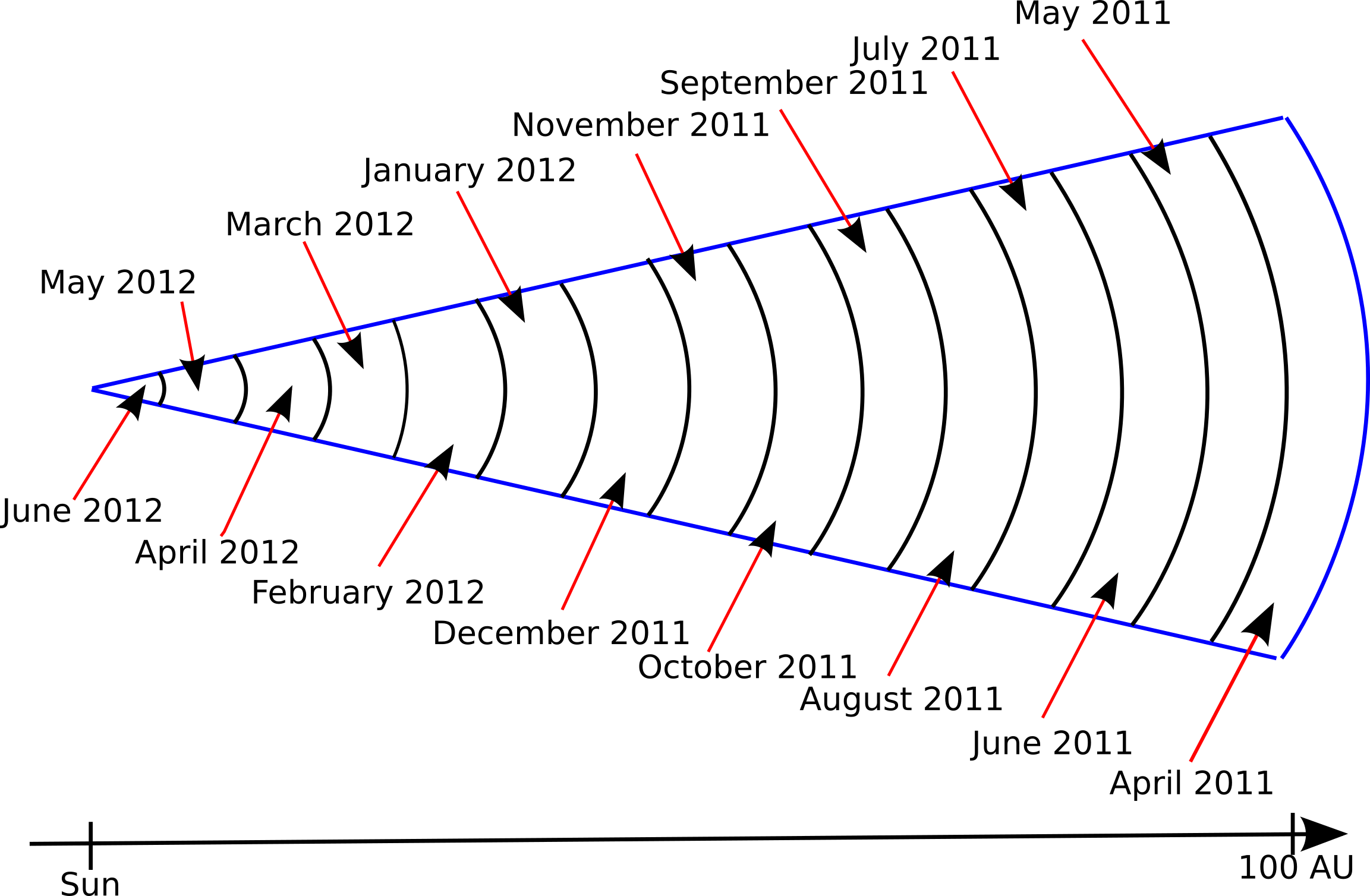
In HelMod model, so far the inner region of the heliosphere was described as an effective heliosphere (Bobik et al 2012) with a radius -- i.e., an effective TS distance -- of 100AU. Solar modulation was, then, treated by subdividing it in 15 radially equally-spaced regions. Each i-th region traveled by CR particles is characterized by heliospheric parameters evaluated at i-Carrington rotations back-in-time, corresponding to the time needed by SW for reaching it (Bobik et al 2012, Boschini et al 2018).
The actual dimensions of the heliosphere are accounted for by scaling the position of TS by the time dependent values obtained as described in Heliospheric boundaries section. The HS is included as a single additional region on top of the 15 inner regions with its actual size as calculated in Heliospheric boundaries section. As discussed in Heliospheric boundaries section the TS and HP latitudinal profile in the nose region was determined taking into account the latitudinal variation of the ISM ram pressure component of the total pressure on the HP surface. In the anti-nose region only the magnetic and plasma pressure were accounted for. As a consequence, an asymmetry in the direction of the ISM flow is introduced (see fig. below). Finally a cylindrical symmetry with respect to the axis along the sun-nose direction was applied to have full three-dimensional heliospheric boundaries.
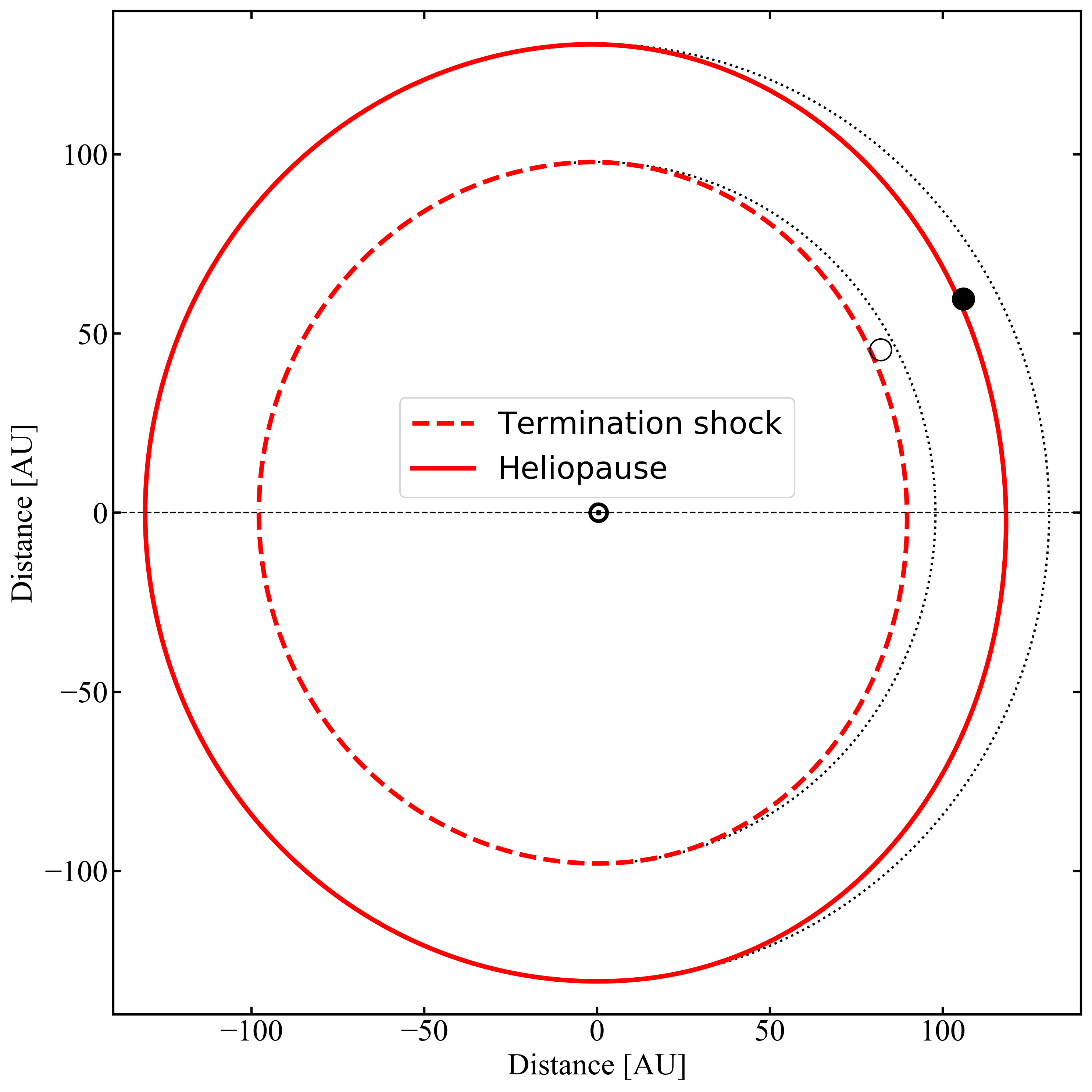
1The inner part of the heliosphere -- corresponding to the space region from the Sun up to the TS -- will be indicated as inner heliosphere in the following.
2The outer part of the heliosphere - corresponding to the space region from the TS up to the HP - will be indicated as outer heliosphere in the following.
3Under the condition that there is no interstellar magnetic field, Parker, (1961; 1963) discussed the case of a steady subsonic interstellar wind leading to a comet-like shape (see, e.g., Axford, 1972; Holzer, 1989, Zank 1999, 2015 and references therein).
Bibliography
 |
Bobik, P., Boella, G., Boschini, M.~J., Consolandi, C., Della Torre, S., Gervasi, M., Grandi, D., Kudela, K., Pensotti, S., Rancoita P.G. and Tacconi, M. (2012). Systematic Investigation of Solar Modulation of Galactic Protons for Solar Cycle 23 Using a Monte Carlo Approach with Particle Drift Effects and Latitudinal Dependence. Astrophys. J., 745:132 . |
 |
Boschini, M.J., Della Torre, S., Gervasi, M., La Vacca, G. and Rancoita, P. G. (2018a) Propagation of Cosmic Rays in Heliosphere: the HelMod Model Adv. Space Res. 62(10):2859 - 2879, 2018 |
 |
Boschini, M.J., Della Torre, S., Gervasi, M., La Vacca, G. and Rancoita, P. G. (2019) The HelMod Model in the Works for Inner and Outer Heliosphere: from AMS to Voyager Probes Observations Advances in Space Research 64(12):2459 - 2476, 2019. |
| Axford, W.I., 1972. NASA Special Publication 308, 609. | |
| Burlaga, L.F., 1984. Space Sci. Rev. 39, 255–316. | |
| Burlaga, L.F., Ness, N.F., 2016. Astrophys. J. 829, 134. | |
| Dialynas, K., et al., 2017. Nature Astronomy 1, 0115. | |
| Drake, J.F., Swisdak, M., Opher, M., 2015. Astrophys. J. Letter 808, L44. | |
| Holzer, T.E., 1989. Annu. Rev. Astron. Astrophys. 27, 199 – 234. | |
| Krimigis, S.M., 2009. Science 326, 971. | |
| McComas, D.J., et al. 2009. Science 326, 959 | |
| NASA-OMNIweb, 2018. online database http://omniweb.gsfc.nasa.gov/form/dx1.html . | |
| NASA-Voyager, 2018. online database https://voyager.gsfc.nasa.gov/flux.html . | |
| Opher, M., Drake, J.F., Swisdak, M., Zieger, B., Toth, G., 2017. Astrophys. J. Letter 839, L12 | |
| Opher, M., Drake, J.F., Zieger, B., Gombosi, T.I., 2015. Astrophys. J. Letter 800, L28. | |
| Parker, E.N., 1958. Astrophys. J. 128, 664. | |
| Parker, E.N., 1961. Astrophys. J. 134, 20. | |
| Parker, E.N., 1963. Interplanetary dynamical processes. | |
| Richardson, J.D., Kasper, J.C., Wang, C., Belcher, J.W., Lazarus, A.J., 2008. Nature 454, 63–66 | |
| Richardson, J.D., 2013. Journal of AdvancedResearch 4, 229–233. | |
| Zank, G., 2015. Annual Review of Astronomy and Astrophysics 53, 449–500. | |
| Zank, G.P., 1999. Space Sci. Rev. 89, 413–688. |